PRNG et générateur de clé
Alors que les grandes nations, autant que les grands groupes d’entrepreneurs, entrent dans une guerre de l’information sans merci. La cryptographie est, plus que jamais, l’arme idéale dans ces conflits. Les algorithmes et la génération de clés sont les piliers de la sécurité de l’information et la cible privilégiée des centres d’espionnage. La NSA l’a compris avec, comme à son habitude, une avance colossale en s’attaquant aux générateurs de clés.
Mais qu’est ce qu’un générateur de clés ? En quoi peut il mettre en péril la sécurité d’un logiciel cryptographique ? Et que cherche un cracker ? A toi mathématicien, cet article te fera découvrir les algorithmes connus de génération d’aléa. A toi développeur, tu pourras jeter un oeil sur l’exemple d’implémentation de ces générateurs. A toi lecteur, tu découvriras ce que cherche un attaquant dans les logiciels de sécurité.
Mettons nous – en situation…
Imaginons que je sois une société développant un jeu logiciel. Je souhaite vendre mon jeu mais je ne veux pas qu’il circule en libre service afin d’éviter que les 6 développeurs qui ont travailler jour et nuit se retrouvent à la rue pour cause de faillite.
Du coup, j’implémente une “clé de sécurité“. En d’autres termes, chaque logiciel se verra attribuer un code alpha-numérique nécessaire à l’installation du jeu.
L’en-jeu
Nous passerons sur le bypass de condition qui est rendu trop compliqué par ces très bons développeurs…et puis ça nous donnera l’occasion de faire un autre billet sur le cracking pour les fans d’assembleur. Mais nous voilà, quand même, confronté à plusieurs questions :
- Comment associer une clé à chaque logiciel ?
- En effet, je ne vais pas, à chaque fois, coder une clé en dur
- Je ne peux pas non plus mettre la même clé sur chaque logiciel, autant ne pas en mettre
- Comment empêcher un cracker de réaliser un générateur de clé (keygen) de mon produit ?
- …arrêtez de faire les innocents on en a tous déjà testé un
KéKonVaFaire
Nous allons donc créer une brique logicielle qui va nous permettre de générer des clés d’activation.
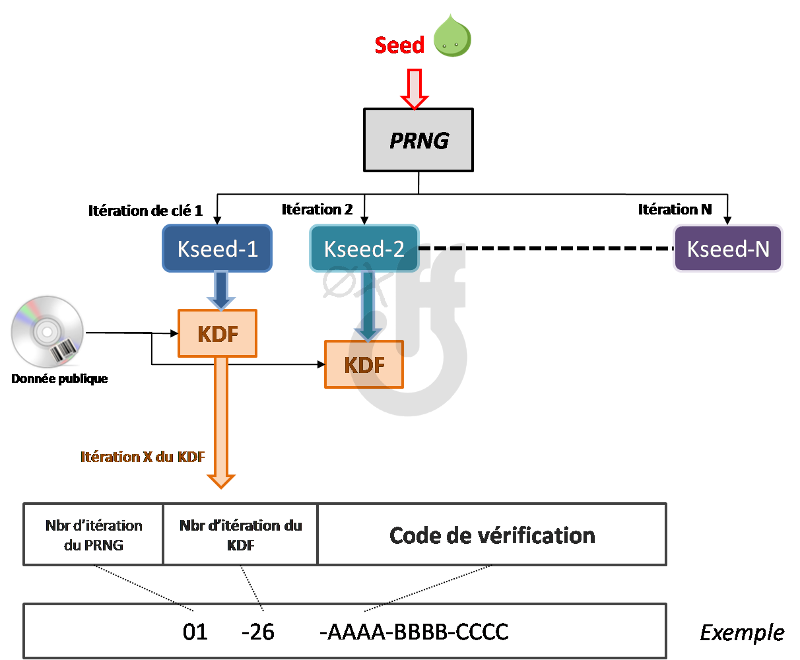
Le principe est le suivant :
- On choisit une graine – seed (une chaine aléatoire de bits)
- On l’utilise pour générer plein de sous clés pseudo-aléatoires – Kseed
- On utilise ces sous clés et une donnée publique pour créer les codes d’activation
“Whahou ! ” Je ne vous le fait pas dire ! Evidemment, dans la suite de cet article nous avons pris un exemple simple. Je vous propose, avant tout, de comprendre ce qu’est une dérivation de clé et les problématiques associées, de mieux appréhender les générateurs de pseudo-aléa (PRNG) et, enfin!, d’améliorer cet article par vos commentaires ainsi que les codes associés par vos corrections. L’union fait la force !
Dérivons, dérivation
Bon, déjà, associons une clé de sécurité à chaque logiciel. Le principe est le suivant : j’utilise une graine (Kseed) que je dérive grâce à une fonction de dérivation (KDF, Key Derivation Function) à laquelle j’ajoute des éléments publiques, comme, par exemple, le numéro de série physique du support. Facile !
Prédictibilité & Cracking
Donc à chaque itération, je vais avoir une nouvelle clé que j’associerais à mes éléments publics. Maintenant, supposons que je sois un vil hacker et que j’ai dans ma besace 200 clés générées avec les codes de série associées.
Mon premier objectif, en tant qu’attaquant, va donc être de trouver une relation entre les codes générées et la donnée publique. Un petit exemple dans l’hyper simplicité :
Mes numéros de série : 1 2 3 4 5 6 Mes clés générées : 1 4 9 16 25 ..
Il n’est pas trop compliqué de connaitre le code généré si votre numéro de série est 6… . Et bien ça, c’est notre problématique de prédictibilité.
Pour les férus de math, en fait, on souhaite une entropie forte sur notre génération de code. Un très bon article sur l’entropie, publié par les étudiants de l’université de Nantes, vous donnera une idée de ce qu’est exactement l’entropie.
En gros, c’est la “capacité chaotique” d’une fonction. Typiquement, je veux que la modification d’un seul bit de mon numéro de série entraîne une nouvelle sortie totalement (pseudo-)aléatoire.
Donc nous allons prendre :
- Une fonction qui nous assure une entropie correcte (SHA256, AES-256,…)
- Un système d’itération indépendant de la donnée publique
L’itération c’est le nombre de fois que je passe dans ma fonction de dérivation. Comme j’aime bien les exemples, je vous propose la fonction de dérivation suivante (RFC5869) :
Ki+1 = SHA256( Ks ^ SHA256 (Ki || Ns || i ) )
Avec :
– Ki est la clé générée à la ième itération
– Ks est notre graine
– ^ est un XOR
– NS est le numéro de série du support physique…que vous pouvez remplacer par ce que vous voulez comme info…c’est toi qui choiz’!
Ce qui nous donne en python (c’est pour la démo) :
#import hashlib def HKDF(Ks, NS, p_i): count = 0 size = len(Ks) concat = hashlib.sha256(str(NS) + "0").hexdigest() #On réalise notre premier XOR idx = 0 xored="" while idx < size : xored = xored + chr(ord(Ks[idx])^ord(concat[idx])) idx = idx +1 #On crée notre dérivation initiale K = hashlib.sha256(xored).hexdigest() #On dérive pour tout le reste while count < p_i: concat = hashlib.sha256(K + str(NS) + str(count)).hexdigest() # On XOR encore et encore, c'est que le début, d'acc... idx = 0 xored="" while idx < size : xored = xored + chr(ord(Ks[idx])^ord(concat[idx])) idx = idx + 1 K = hashlib.sha256(xored).hexdigest() count = count + 1 return K ##MAIN Ks = hashlib.sha256("Kseed") NS = "0001234" iter = 4 print(HKDF(Ks, NS, iter))
Bon là évidemment on se retrouve avec des clés du style :
31f7a65e315586ac198bd798b6629ce4903d0899476d5741a9f32e2e521b6a66
Perso, un jeu qui me demande d’entrer ça à la main, je ne vais pas beaucoup l’aimer. DONC ! on va faire une sorte de traducteur.
Le traducteur
Le problème du traducteur c’est qu’il ne doit pas diminuer le niveau de sécurité initiale. Donc on va faire un simple encoding en base64 parce qu’on est très feignant, mais dans l’absolu, il est préférable d’éviter tout ce qui peut vous donner des caractères autre qu’alphanumérique. Ce qui nous donne :
#import base64 def traduction (hash) : b64code = base64.b64encode(hash) size = len(b64code) idx=6 while idx < size: code = code + b64code[(idx-6):idx]+"-" idx = idx + 6 return code[:-1]
Alors c’est encore très long, vu qu’on a choisi une clé sur 256 bits mais essayez avec un sha1 ou un md5, vous devriez trouver quelque chose d’exploitable. Vous pouvez aussi garder les valeurs hexadécimal…c’est vous qui choisissez ce que vous préférez !
Reste encore une dernière question, comment générer ma graine (seed) de départ?…
Petite note sur la périodicité
Le cycle d’un générateur de clé c’est le nombre de clés qu’il peut générer. Il faut savoir qu’un HKDF, tout comme le PRNG, est un automate déterministe. Si j’ai la même graîne et le même nombre d’itération, je vais avoir la même sortie. La question est donc au bout de combien d’itérations je retombe sur une dérivation connue.

Ici, nous n’avons pas réaliser de tests mathématiques sur la périodicité mais sachez que c’est ce que l’on reproche à la NSA (et là aussi). On accuse, en effet, la NSA d’avoir forcer l’implémentation de certain générateur de pseudo aléa afin d’avoir un nombre restreint de clés à tester.
Grossièrement, votre rand(0, 2256) ne vous génère que 216 clés (ou une suite de clés prédictibles). Du coup si je récupère votre message chiffré, je n’ai que très peu de clés à tester. Ils sont malins ces américains !
La génèse de la clé
Un générateur de pseudo-aléa (ou PRNG Pseudo-Random Number Generator), est, comme précisé plus haut, un automate déterministe. Et c’est exactement ce que l’on cherche puisque nous souhaitons “maîtriser” la génération d’aléa. Bah oui ! C’est bien beau de générer un aléa mais si je ne suis pas capable de le retrouver, je ne vais pas pouvoir vérifier mon code d’activation.
Et c’est là que le PRNG est génial, puisqu’il va me générer un aléa par itération. Du coup je n’ai qu’à connaître le nombre d’itération pour retrouver l’aléa. Et, propriété bonus, il n’y a pas de relation déductible entre un aléa1 et un aléa2.
Nous allons en voir 3, le LFSR (Left Feedback Shift Register), qu’on a vu rapidement dans un précédent article, Blum Blum Shub que nous allons découvrir… Joie ! Et le PRNG-RSA, simple et efficace.
Pour ceux que ça n’intéresserait pas, vous pouvez générer une graîne avec la commande ci-dessous et passer à la suite :
# Vous pouvez mettre ce que vous voulez à la place du 256 évidemment :)
Ks = os.system('cat /dev/urandom | tr -dc [a-zA-Z0-9] | head -c 256')
Le LFSR
Pourquoi commencer par LFSR ? Et bien parce que le procédé est un parfait exemple de génération de clé synchronisée. Le principe est le suivant :
- Alice et Bob partage une graine
- Alice dérive sa graine N fois et génère une clé
- Alice envoie sa clé à Bob
- Bob dérive N fois sa graine (partagée)
- Bob vérifie que la clé récupérée est bien celle envoyée par Alice
Le nombre N peut être un compteur ou une marque de temps.
De façon plus précise, un LFSR va générer une clé “en continue“. C’est à dire qu’il va générer une clé bit à bit et, tout ça, dans un espace défini. C’est comme une file (FILO), le bit de clé qui va chiffrer sort, un nouveau bit est alors créé et se met en queue. On utilise pour ce faire, ce qu’on appelle, un polynôme de rétroaction. Explication en image.
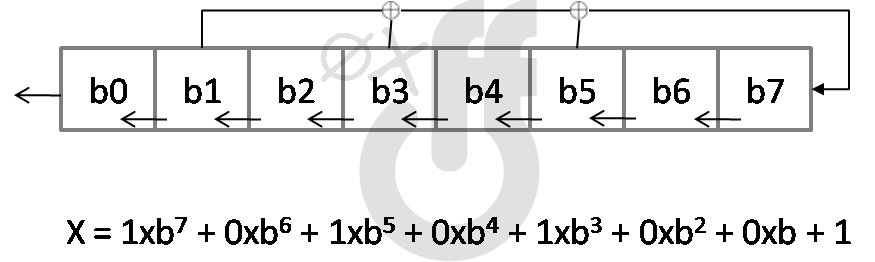
L’inconvénient est d’éviter les répétitions. Donc un simple XOR des bits de clé sortant nécessite des cycles au moins aussi long que le message. C’est notre problème de périodicité. Pour plus de détail sur le LFSR, je vous laisse ce PDF de l’université de Lille très bien fait ainsi que ce lien de l’INRIA.
def LFSR(seed) : # Ici, la graine est un tableau de 8 bits coef = seed size = len(coef) # Notre polynôme : P = X7 + X5 + X3 + 1 pol = [1,0,0,1,0,1,0,0] # On fait un tour complet # C'est à dire que l'on va faire tourner le LFSR pour chaque bit de seed j = 0 while j < size: i = 0 # Notre Polynome est sous la forme coefi*Xi # x = 1*X7 + 0*X6 + 1*X5 + 0*X4 + 1*X3 + 0*X2 + 0*x1 + 1 x = coef[i]*pol[i] i = i + 1 while i < size : x = int(x)^int(coef[i]*pol[i]) i = i + 1 # On sort le premier bit (on décale à gauche --Left Shift ;)) # et on ajoute, à la fin, celui qu'on vient de calculer for i in range(0,(size - 1)): coef[i]=coef[i+1] coef[size-1] = x^1 j = j + 1 return coef ### MAIN seed = [1,1,0,0,1,1,1,1] res = LFSR(seed)
“Bah c’est génial ça ! C’est quoi le problème ?“. Et bien le problème, c’est que notre LFSR est une suite d’équation linéaire, du coup, je sais que le dernier bit du LFSR de sortie est le résultat d’un polynôme des autres bits. Ainsi avec assez de couple {clair,chiffré} je peux retrouver mon polynôme de génération.
BONUS : Cet article, trouvé à la dernière minute, montre un exemple de crack d’un PRNG LFSR intentionnellement faible dans le cadre d’un challenge crypto, à lire pour ceux que ça intéresse.
Blum Blum Shub
Cet algorithme dont le nom ressemble à une marque de chewing-gum est un incontournable en PRNG. Il est considéré comme sûr si, et seulement si, on suit à la lettre les recommandations théoriques.
Le principe est le suivant :
Ki = (K)2 mod M
Avec :
– M = p*q
– p et q premiers
– p ≡ 3 [4] , q ≡ 3 [4] (p et q congru à 3 modulo 4, résidu quadratique)
– Le PGCD(Φ(p,q)) est le plus petit possible
Ok donc en se basant sur cet article assez sympa nous pouvons dégager notre structure en python :
def BBS(p_start , p, q, p_i): M = p*q x = p_start count = 0 while count < p_i: x = (x*x)%M #Ki = K^2mod M count = count + 1 return x
Les premiers seront…
Voilà, ça c’était la partie facile, maintenant il faut générer des premiers qui respectent les considérations vues plus haut. Je vous laisse regarder ce premier code largement inspiré de ce très (TRES) bon site de crypto pour python.
#import math #Cherche les 'premiers' < n _prime=[2,3,5,7] _quadra=[3] def get_prime(n): global _prime, _quadra p = _prime[-1] # On prend le dernier premier connu p = p + 2 # On évite les nombres paires while p < n : if is_prime(p): _prime.append(p) #Si p est premier, on l'ajoute à la liste #si en plus il répond à la clause de résidu quadratique #on l'ajoute dans la liste if p%4 == 3 : _quadra.append(p) p = p + 2 def is_prime(n): if n == 2 : return 1 # 2 est un premier if n < 2 : return 0 # Si t'es inférieur à 2 tu sors stop = math.floor(n**0.5) # On teste pour tout les premier < √n for i in _prime: if i < stop : if n%i == 0 : return 0 # n divisible <=> n pas premier else : break return 1
Voilà une méthode sympa et sûr mais très très très longue si on veut générer une clé sur un ensemble M de quelques centaines de bits. Du coup on triche un peu et on utilise ou bien les nombres premiers de Mersenne. Grâce au projet GIMPS, nous avons à disposition une liste de premier que nous pouvons utiliser. Dans le même esprit, vous pouvez aussi utiliser les nombres de Cullen ou de Woodall.
Ou alors, et c’est quand même vachement conseillé, nous pouvons générer un aléa et faire un test de primalité comme celui de Fermat, ou celui de Miller–Rabin mais Fermat est hyper plus simple. J’en profite pour remercier drgoulu avec son bel article en français.
Ce que dit Fermat c’est que quelque soit a, si :
- 1 < a < n-1
- pgcd(a,n) = 1
- a(n-1) ≡ 1 [n]
…alors n a de forte chance d’être premier. Un petit exemple avec 5 :
14 = 1 [5] 24 = 16 = 1 [5] 34 = 81 = 1 [5] 44 = 256 = 1 [5]
Il est fort ce Fermat ! Petit bémol quand même, car il existe des nombres qui remplissent cette condition et qui ne sont pas premiers, les nombres de Carmichael, mais ils sont vachement rares.
#import random PRECISION = 30 def fermat(n): e = n - 1 if (n==2) : return 1 if (n%2==0) : return 0 for i in range(0,PRECISION) : a = random.randrange(2,n) ## Si a divise n...bah c'est que n est pas premier if (n%a == 0 ): return 0 ## Si a(n-1) !≡ 1 [n] alors c'est un composite res = (a**e)%n if res != 1: return 0 return 1 def gen_alea(n) : #On génère n-1 bits aleatoires alea = bin(random.randint(0,1)) stop = n-1 for i in range(stop): alea = bin(random.randint(0,1)) + alea[2:] #On ajoute un pour être sur qu'il soit impair alea = alea + bin(1)[2:] alea = long(alea,2) return alea ##GENERER un nombre premier ça donne : def gen_prime(): alea = 4 while (fermat(alea) == 0 ): #On genere l'alea de 16 bits alea = gen_alea(16) # On test s'il est premier if fermat(alea) == 1 : print(str(alea) +" semble être un premier !") return alea
Génial ! On a un algo qui marche pour des grands nombres. Moins génial ! On va avoir une petite limitation python. Oui vous pouvez essayer en augmentant le nombre des X bits aléatoires, python a un peu de mal à faire des exponentiations. Du coup, on utilise un programme plus bas niveau comme le C avec une librairie gmp. Ici je laisse l’exemple en python car c’est bien plus facile à comprendre mais pour les curieux un lien vers le dev en C est ici.
Est ce qu’on pourrait pas résumer simplement ?
Si si si, vous avez raison, avec toutes ces problématiques de nombres premiers on en oublie un peu notre BBS. Donc pour résumer ! En algo, et avec la version PRBG (Pseudo-Random Bit Generator), ça nous donne :
1) Tant que p[4] ≠ 3[4] : générer un premier p #Ici on considère que 3 est un PGCD acceptable pour les totients d'Euler 2) Tant que q[4] ≠ 3[4] et pgcd((p-1),(q-1)) > 3 : générer un premier q 3) M = p*q 4) Générer un alea K //ou un premier aussi 5) Tant que i < Nombre_de_round : K = K*K mod M out[i] = X bits de poids faibles 6) Alea de sortie = out[]
Le BBS est considéré comme l’un des plus sûr générateurs de pseudo aléa. Cependant, un article très haut niveau est disponible sur la considération de sécurité de BBS et met en cause cette sécurité si le modulo M choisi n’était pas assez grand. Haut niveau car là, j’avoue, je m’y suis pas mal perdu, mais jetez un oeil au moins sur la conclusion. Et si tu es mathématicien, n’hésites pas à nous dire ce que tu en penses, nous t’en serons infiniment reconnaissant.
PRNG-RSA
Bon déjà reprenons, PRNG-RSA c’est son petit nom sexy mais son vrai nom c’est Micali-Schnorr PRBG (pseudo-random bits generator)…tout de suite moins sexy quand même. Ici, il semble que l’affaire du modulo est moins problématique, sinon le principe est le même avec un exposant différent de 2.
Xi = (X)e mod M
Ki = N bits de poids faible de X
K = K0 || K1 || K2 ||…|| Kfinale
Avec :
– M = p*q
– p et q premiers
– 1 < e < (p-1)(q-1)
Si vous avez compris le BBS, il suffit de l’appliquer au RSA. Vous pouvez aussi regarder le code commenté disponible sur le partage.
Oui MAIS !!
Oui alors c’est bien gentil tout ça mais, là, le vil pirate qui me vole ma graine (seed) peut générer toutes les clés qu’il souhaite. Et bien vous avez tout compris ! Et soyons clair, un attaquant motivé trouvera ! Mais ce n’est pas une raison pour lui faciliter la tâche.
Complication par l’obscur
Ici, nous allons faire en sorte de rendre l’algorithme de récupération de graine plus complexe que d’ordinaire. Ce n’est pas une mesure de sécurité !!! Mais cela nous permet de supprimer une population d’attaquant comme les script-kiddies et attaquants faibles.
1 – Éviter le strings !
Vous connaissez tous cette commande qui permet de lire toutes les données en clair dans votre programme. Si vous ne connaissez pas, voilà un petit exemple à faire chez soi :
Code1.c
#include <stdio.h>
#include <stdlib.h>
#define TEST "unsecret"
int main(){
char test[14]="unautresecret";
memset(test,0,14);
strncpy(test,TEST,8);
return 0;
}
-------------------------------
#>gcc -o test Code1.c
#>strings test
Vous comprenez que si on met notre graine comme ça dans une variable…c’est un peu facile pour l’attaquant. Une idée est de calculer vos valeurs sensibles à la volée. Vous pouvez réaliser différents XOR, passer par une matrice de permutation, etc. Ici, il faut rester assez discret pour ne pas attirer l’attention via le strings.
2 – Éviter le trivial !
Là, évidemment, tout dépend de votre notion de trivial. En fait, il faut que ce soit assez compliqué dans votre suite d’instruction lorsque votre attaquant essaiera de faire du reverse mais facile à maintenir niveau code. Objectif : rendre la lecture en assembleur ou la lecture “step by step” complexe.
Dans l’exemple sur github, vous verrez que j’emploie un simple XOR avec en clé des noms de fonctions. Evidemment trop simple, mais suffisant pour l’exemple.
3 – Tenter l’obfuscation de code
Si vraiment vous ne faites confiance à personne, vous pouvez utiliser des astuces d’obfuscation comme mettre des noms de variables étranges et des valeur en hexa. Il y a même des obfuscateurs en ligne…enfin si vous leur faites assez confiance pour leur présenter votre code, sinon il faudra en télécharger un.
Le petit plus, le certificat
Pour encore plus de sécurité, je peux mettre en ligne un service de signature de configuration. En gros, au lieu d’entrer directement sa clé de sécurité dans le jeu, le joueur va s’inscrire sur mon site et entrer sa clé. Mon serveur va vérifier que sa clé est valide et envoyer un fichier de configuration contenant :
- Sa nouvelle clé de sécurité
- Qui pourra être basée sur l’adresse MAC du PC du joueur par exemple
- Des informations relatives au joueur
- Nom Prenom
- Adresse mail
- …
- Une signature de ce fichier réalisé par un certificat de ma compagnie
Avant l’installation, mon programme va vérifier ce fichier de configuration et lancer l’installation si la signature ET la clé sont valides.
Une connexion internet sera obligatoire pendant l’installation pour vérifier la validité du certificat.
Pour les paranoïaques, vous pouvez répéter l’opération à chaque utilisation…par contre si vous êtes strict sur la vérification de la CRL, un utilisateur qui n’a plus internet, ne peut plus utiliser votre produit. Pour un petit rappel sur l’utilisation des certificats, n’hésitez pas à faire un petit saut ici.
En espérant que ça vous ait plu ! N’hésitez pas à poster vos commentaires : la force d’une communauté se mesure à sa capacité de partage.